Voxels within a Euclidean sphere of radius R are defined on a Cartesian grid as √(x2+y2+z2) < R where R is the distance to the center of the neighboring voxel. Euclidean spheres can be used to restore a 3D shape from its medial surface (thinning the medial surface to a medial axis is a lossy process and is not reversible by sphere drawing). Euclidean spheres are also useful in constructing random porous media.
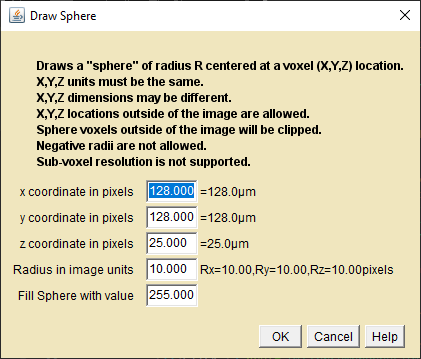
The Euclidean Spheres plugin operates on 3D images with symmetric or asymmetric voxels. The sphere radius is in image units. The drawn sphere surface is not drawn with sub-voxel resolution, i.e. if a voxel's distance from the origin pixel is greater than R it is not filled. A sphere that has an origin outside of the volume will be clipped, showing only the portion within the volume.


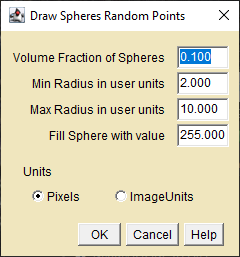
Similarly, the Overlapping Spheres plugin operates on 3D images with symmetric or asymmetric voxels and the sphere radius is in image units. It draws overlapping spheres with random radii at random locations to a required volume fraction. Random locations are seeded with the last 5 digits of the system millisecond clock so they are unlikely to repeat very often. High volume fractions may fail with an error message if the plugin cannot find an unfilled location to draw the next sphere.